Partial cubes from rhombus tiling flips
I'm very interested in a recently updated arXiv paper by Bodini, Fernique, Rao, and Remila, "Distances on Rhombus Tilings", arXiv:0911.2804. It finds yet another example (like the one in my "happy ending" paper) of a family of flip graphs that are automatically partial cubes.
To review: a partial cube is a graph whose vertices can be labeled by bitvectors in such a way that graph distance is the same as the Hamming distance between the labels. They are equivalently the graphs that can be drawn in a distance-preserving way in an integer lattice of some dimension. When a large state space, such as the space of all triangulations of a point set, can be represented as a partial cube, that's a good thing, because it allows distances between pairs of states to be calculated by looking only at the bitvectors of those states without having to search through the entire state space for a path.
The state space Bodini et al look at can be described in several different equivalent ways. The most concrete is that they have a convex polygon with pairs of axis-parallel sides, such that the two sides in each pair have equal integer lengths. Every polygon of this type can be tiled by rhombi with unit side lengths, and every rhombus tiling is itself a partial cube, but that's not what the new paper is about. The issue is rather that there may be many tilings of the same polygon, so we can build a big state space that has a vertex for each different tiling and an edge connecting similar pairs of tilings. Three rhombi meeting at a common vertex to form a convex hexagon may be replaced by a different set of three rhombi, and this move is called a "flip". The question is, how many flips does it take to get from one tiling to another, or in other words, what is the distance between tilings in this flip graph?
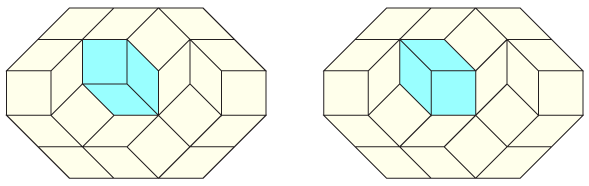
There's an equivalent way of describing rhombus tilings, as pseudoline arrangements, that is more helpful for describing the bitvector labelings of this state space. If one draws short curves within each rhombus, connecting pairs of opposite edge midpoints, then these curves join up to form a pseudoline arrangement: a family of longer curves that can be extended to infinity in both directions, with each two curves crossing each other at most once. The curves in the arrangement form bundles of parallel pseudolines (curves that don't cross each other at all), one bundle for each pair of parallel sides of the polygon. And conversely, if you have any simple pseudoline arrangement (one where only two lines meet at each crossing), then you can group its edges into bundles and turn it into a rhombus tiling by making a rhombus for each crossing, with the shape and orientation of the rhombus determined from the identities of the parallel bundles of the crossing lines.
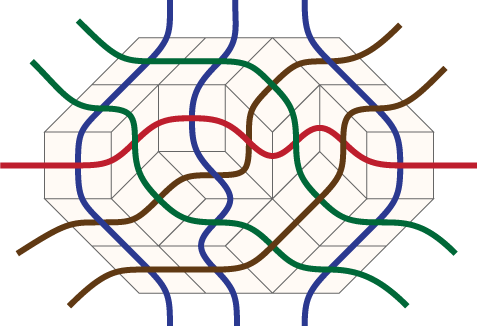
So far, this is all standard. It's also standard to consider these tilings and arrangements as being equivalent to a third kind of object, an oriented matroid of rank three, and that's where the bitvector labeling comes from. (Let's leave out the fourth standard equivalent type of object, circular sequences of permutations.) The coordinates of the labeling are determined by triples of lines that all intersect each other. For each such triple, there are two possible orientations of the triangle that they form: if we assign an arbitrary orientation to each of the lines, then it may pass either to the left or to the right of the triangle, but there are only two consistent ways of choosing, for all three of the lines, whether they pass to the left or to the right. We simply set that bit of the label to 0 if the triangle is in one of the two orientations, and to 1 if it is in the other orientation.
Since each flip operation changes a single bit of this encoding, the Hamming distance between bitvector labels is always greater than or equal to the flip distance between tilings. What Bodini et al show is that, in some cases, these two distances are necessarily equal: one can be guaranteed to be able to find a sequence of flips in which there is no wasted efford, in which every triangle flipped is one for which the two tilings have different orientations. Specifically, this is true when the initial polygon has six or eight sides (that is, when the pseudoline arrangement has three or four bundles of parallel lines), when there are ten sides but one pair of parallel sides has length one, or when there are ten sides but all pairs of parallel sides have length two. In all other cases there are tilings that are farther apart than their Hamming distance would indicate. In a previous conference version of their paper, the authors had conjectured that all polygons with ten sides have partial-cube flip graphs, but they disproved their own conjecture by doing a big computer search for obstacles (minimal triangles that are inverted from each other in two different pseudoline arrangements, but that can't be flipped because they are not faces of the arrangement).
There is also some connection here to the theory of regular labelings, which can be used to give a distributive lattice structure to certain sets of geometric objects. The underlying graph of a distributive lattice is necessarily a partial cube – by Birkhoff's representation theorem, a distributive lattice can be represented as the family of lower sets of a partially ordered set, and the distance in the graph of the distributive lattice is just the Hamming distance between lower sets – but, as Bodini et al state, one gets a distributive lattice structure only for tilings of six-sided polygons. So there is some intermediate region in complexity, including the eight-sided polygons, where one has a partial cube structure that does not come from a distributive lattice. It would be of interest, I think, to determine whether in these cases it is at least still a median graph rather than some other kind of partial cube that has even less structure.