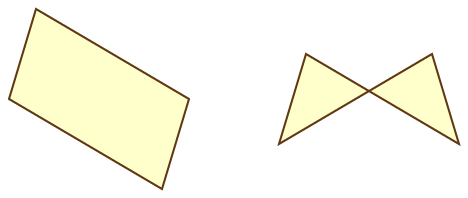
Flex-invariant families of quadrilaterals
It's time to do some more elementary geometry!
An orthodiagonal quadrilateral is a quadrilateral whose two diagonals lie on perpendicular lines. A tangential quadrilateral is one whose four sides lie on lines that are tangent to a common circle. (I've tried to word these definitions carefully so they work correctly even for nonconvex quads.)
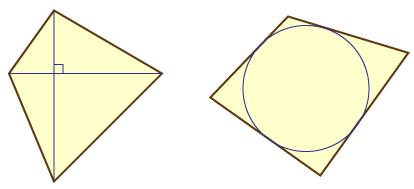
Now, suppose you make one of these quadrilaterals so that the sides are rigid but the corners are hinged, so that the whole thing forms a flexible four-bar linkage. If you make a linkage in the form of an orthodiagonal quadrilateral, and flex it, it will always stay orthodiagonal, even though its shape will change. Perhaps even more surprisingly, if you make a linkage in the form of a tangential quadrilateral, and flex it, it will always stay tangential!
Trick question: if you make a linkage in the form of a parallelogram, and flex it, will it always stay a parallelogram?
One way of explaining these facts is that the orthodiagonal and tangential quadrilaterals can both be characterized by similar-looking formulas in terms of the lengths \( a, \) \( b, \) \( c, \) and \( d \) of their sides (in clockwise order). In an orthodiagonal quadrilateral, it follows from the Pythagorean theorem (applied to the four right triangles that the two diagonals split the quad into) that \( a^2 + c^2 = b^2 + d^2, \) and conversely any quadrilateral in which this is true must be orthodiagonal. Similarly, in a tangential quadrilateral, each triangle formed by one of the quadrilateral's corners and the two adjacent points of tangency of the inscribed circle must be isosceles; it follows from this that \( a + c = b + d, \) and conversely any quadrilateral in which this is true must be tangential. Since \( a, \) \( b, \) \( c, \) and \( d \) don't change when a four-bar linkage is flexed, these equations are invariant under flexing and orthodiagonality or tangentiality is preserved.
Another class of quadrilaterals that is invariant under flexing is the kites, quadrilaterals in which one of the diagonals is an axis of symmetry. A kite can be characterized by the two equations \( a = b \) and \( c = d. \) However, a different pair of equations, \( a = d \) and \( b = c, \) also defines a kite, with a different axis of symmetry. It turns out that the kites are exactly the quadrilaterals that are both orthodiagonal and tangential. In one direction, it's obvious that if one of the two sets of kite equations is true, then the orthodiagonal and tangential equations are also true. In the other direction, a little algebra shows that if the orthodiagonal and tangential equations are both true, then \( (a-c)^2 = (b-d)^2. \) If one takes square roots of both sides, there are two different cases to consider: the square roots can both have the same sign, or they can have opposite signs. In either case, one gets two linear equations in the four unknowns: the tangential quadrilateral equation and the equation from the square roots. Solving these simultaneous equations gives in the two different cases the two different sets of kite equations.
Ok, finally, the answer to the trick question: yes and no. Like a kite, a parallelogram is defined by two equal pairs of side lengths, but in a parallelogram the equal sides are opposite each other rather than adjacent. And most of the time when you flex a parallelogram it will remain a parallelogram. But if you stretch two opposite corners as far apart as possible (so that the edges of the parallelogram stretch to all lie on a single line) you can get from that configuration to a different configuration, with crossed edges, called an antiparallelogram. So the class of parallelograms and antiparallelograms is closed under flexing, but parallelograms can turn into antiparallelograms or vice versa.