I've been working on an implementation of the circular layouts of regular graphs from my Lombardi drawing paper, and came across the following really pretty layout of the Folkman graph, a graph with the curious property that its edges are all symmetric to each other but its vertices aren't. I don't have that much more to say here about the graph, and the software could probably stand to be tested a bit more thoroughly before sharing, but I thought I would at least share the picture:

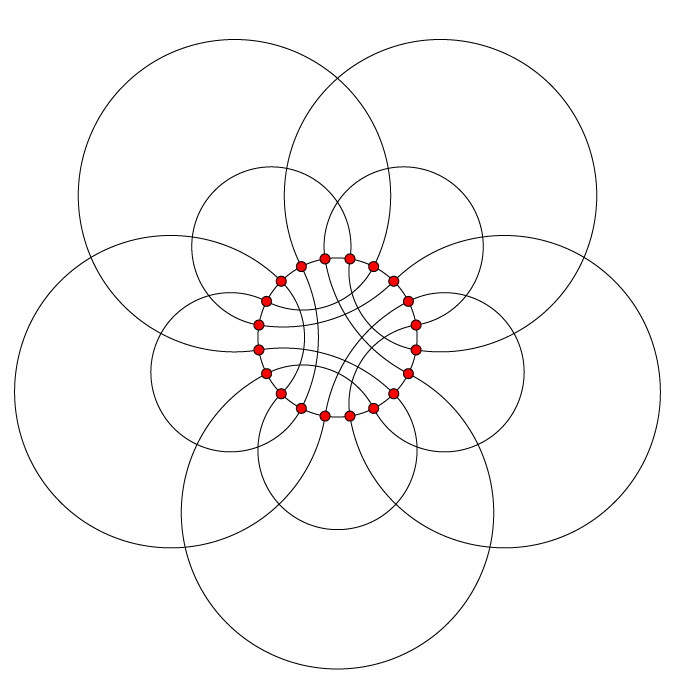
Lombardi drawing of the Folkman graph

ETA 2010-11-29: Here is the implementation.




Comments:

None:
2010-10-15T06:41:08Z

So I'm not much of an appreciator of graphs. Only a select few graphs have an aesthetic that tickles me - these are usually unique Ramsey graphs with a lot a symmetry (and usually self-complimentary).

Just wanted to drop by to say that this visualization is one of the few that inspired in me an appreciation of graph elegance in the way I imagine a lot of graph/Ramsey theory people must all of the time.

None:
2010-10-15T06:43:15Z

(Please forgive my abuse of the English language; my only defense is that it's close to three in the morning for me and I just finished a 9 hour blitzkrieg on my mounds of problem sets)

ext_174548:
2010-10-15T12:08:32Z

That really is a beautiful and intriguing object!