Graph h-indices and fast ERGM simulation
The first of my WADS acceptances is up as an arXiv preprint: The h-Index of a Graph and its Application to Dynamic Subgraph Statistics (with Emma Spiro, a beginning graduate student in Sociology here at UCI). It combines two subjects that were already familiar to me, dynamic graph algorithms and subgraph isomorphism, with some others that are a little farther afield from my past research: social network analysis, exponential random graphs, and Markov Chain Monte Carlo simulation.
The context is the analysis of social networks. One often thinks of these things as being big graphs with power-law properties; maybe this is true of networks such as LiveJournal's friends links or Google scholar's citation database, but Carter Butts (Emma's advisor) likes to emphasize that there's plenty of interesting information to be gained from smaller networks on the scale of a department or research specialty or school class, where power laws don't really apply. We'd like to come up with mathematical models of these networks that are variable enough to capture the differences between social networks, but with few enough parameters that we can fit the models to the data, and a popular and powerful tool for this is the exponential random graph.
The exponential random graph model (ERGM) is a way of describing probability distributions on sets of graphs. One defines certain features that can be recognized in graphs on a given vertex set, with a weight for each feature: for instance a feature might be an edge, a vertex with a given degree, or something more complicated. Among all graphs on a given fixed vertex set, one defines the log-likelihood of each graph to be the sum of the weights of its features. That is, the probability of a graph is an expression of the form \[ \frac{\exp\sum f_i w_i}{Z}, \] where \( f_i \) is a 0-1 variable that indicates whether feature \( i \) is present in the given graph, and \( w_i \) is the weight of that feature. \( Z \) is a normalizing constant needed to make the total probability come out to one; it can be computed in principle though not in practice by summing expressions of this form over all graphs on a given vertex set. For instance, if the only features are individual edges and they all have the same weight, we recover the familiar \( G(n,p) \) model for random graphs, while features for vertices with given degrees allow the model to control the degree distribution of the graph. With sufficiently complicated features, exponential random graphs can determine any probability distribution, but usually the features are simple, such as the presence or absence of small subgraphs within the graph.
In order to do any kind of probabilistic reasoning in these models (such as fitting the weights to real-world data) one needs to use Markov Chain Monte Carlo simulation, in which a randomized algorithm repeatedly performs small changes to the graph and accepts or rejects these changes depending on a change score that describes how the change would affect the log-likelihood of the resulting. Fortunately this method doesn't need to know \( Z \) a priori (in fact, computing an approximation to \( Z \) is one of the simpler tasks that can be solved in this way). As the inner loop of the algorithm, computing change scores needs to be fast, and it needs an exact rather than approximate change score. That's where the new algorithms of the paper come in: we show how to quickly compute change scores for dynamic graphs, using any kind of feature defined as the presence or absence of an induced subgraph with at most three vertices in the given graph. The algorithm can also handle graphs with labeled vertices: for instance in graphs representing sexual contacts between people, contacts representing different combinations of genders would have different statistics, and should be represented by ERGM features with different weights.
The \( h \)-index of the title comes from a method proposed by Hirsch for evaluating the impact of a scientific researcher while not being overly influenced by publication records full of many low-impact papers or a small number of very high impact papers. It's defined as the maximum number \( h \) such that the researcher has publisher \( h \) papers that each have at least \( h \) citations. While there's some reason to be skeptical that it's measuring the right thing (I'd rather have one new paper that earns 250 citations than five new papers that earn 50 each, even though the latter would be much better for my \( h \)-index), one can treat it purely as a mathematical quantity and examine its behavior in a broader context. In this paper we generalize \( h \)-indices to arbitrary graphs; we define the \( h \)-index of any graph to be the maximum number \( h \) such that some set of \( h \) vertices each have degree at least \( h \). For instance the graph below has \( h \)-index 4: the four red vertices each have degree four or more, and there are no five vertices with degree five or more.
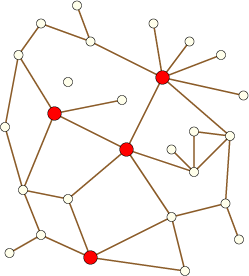
The \( h \)-index is sandwiched between \( 2m/n \) and \( \sqrt{m} \), and (as we show) can be maintained in a dynamic graph in constant time per update. Our algorithm for computing ERGM change scores is based on this idea of picking out a small number of high-degree vertices, which it handles differently from the many low-degree vertices in the graph, so the \( h \)-index shows up both in the algorithm itself and in its analysis; it takes \( O(h) \) time per update. We also ran experiments computing the \( h \)-index of many real-world social networks, in order to estimate how well our algorithms would work on ERGMs with similar structure; curiously, we found that the \( h \)-index seems to be bimodally distributed, behaving as a power of \( n \) with a smaller power for some graphs and larger for other graphs. It would obviously be of interest to understand better what causes this bimodal behavior.
ETA: Coincidentally, soon after mine, another paper on triangle counting, describing fast approximation algorithms for the problem, appeared on the arXiv. It's not suitable for the ERGM application because the MCMC simulation needs exact rather than approximate change scores, but similar subgraph census problems occur in other applications including bioinformatics, so this new paper should be more useful there.