Usually when I put up a new preprint on my web site or the arXiv, I'll mention it here, but today I'm instead going to plug two of my papers that I haven't yet put on my web site. They're both ones that have appeared in print recently, though. Both are the results of some quadrilateral meshing research that I did a year ago with Mike Goodrich, Ethan Kim, and Rasmus Tamstorf, while Mike and I were consulting for Disney Feature Animation and Ethan (a student of Sue Whitesides at McGill) was interning there.

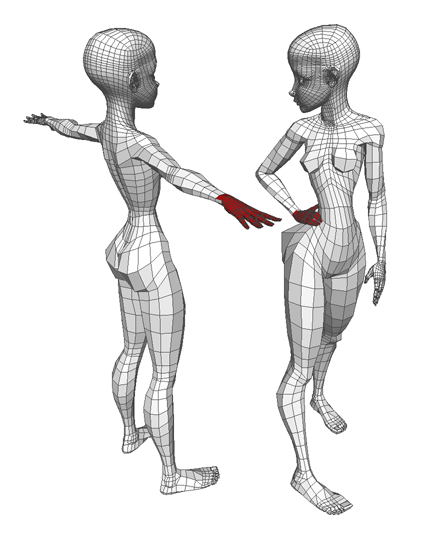
The model girl shown below explains a lot about the problems we were working on. I'm not exactly sure which movie she's from, but as can be seen in the image Disney uses quadrilateral meshes for the 3d models in their computer-animated movies. Two models that might appear very different (representing different characters in the movies) might actually have the same incidence structure of quadrilaterals, and two models that might appear the same (the girl's two poses) might actually differ structurally (her hand has been separated and reattached in a different way to the rest of the model) but have large matching regions. In order to save work in later stages of animation, such as painting the surfaces of the model, it's important to be able to find these matching regions.

Two poses of the same figure with nearly-isomorphic meshes

In our paper “Approximate Topological Matching of Quadrilateral Meshes,” which Mike presented in early June at the IEEE International Conference on Shape Modeling and Applications, we directly address this matching problem. We prove some NP-hardness results, and show that some obvious greedy approaches in which one grows a match between a pair of regions on two similar models one quadrilateral at a time can be badly misled. But our main result is a heuristic approach in which we grow matches between pairs of regions even more greedily, by adding contiguous blocks of quadrilaterals that are all adjacent to the previously matched regions. As we show, if the two models differ only by some small well-separated defects, this method will find the correct match between the rest of their meshes, and it also seems to work well in practice. I haven't put this one online yet mostly because we're working this month on revising this paper to make a journal submission.

The other paper, “Motorcycle Graphs: Canonical Quad Mesh Partitioning,” was presented by Rasmus at the Eurographics Symposium on Geometry Processing last week. In the girl model above, and in many of the models in this application, the mesh is semi-structured: it has irregular vertices, where three, five, or even more than five quadrilaterals meet, but most of the vertices are regular, having exactly four neighboring quadrilaterals. (A vertex on the boundary with exactly two neighboring quads is also considered regular.) In this paper, we look at problems of cutting meshes into a small number of structured submeshes in which all vertices are regular. To do so, we adapt the motorcycle graph idea that Jeff Erickson and I had previously used to analyze straight skeletons.

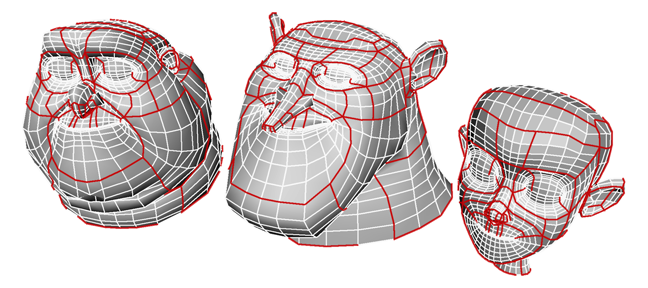
The motorcycle graph construction was in turn inspired by a game from the Disney movie TRON, in which players ride “light cycles” that leave tracks that form barriers for the other players. In a motorcycle graph, a system of particles move in straight lines until they collide with the track left by another particle, at which point they stop. We apply this idea to quadrilateral meshes by starting particles moving outwards from each edge at each irregular vertex, and by defining “move in straight lines” to mean that when one of these particles enters a regular vertex, it exits on the opposite edge. One important detail is that, if two particles reach a vertex at the same time, we have to break ties, which we do using the familiar right hand rule from four-way traffic stops. The tracks left by the motorcycles turn out to partition the mesh into structured submeshes, within a constant factor of optimality by various natural quality measures (though not unfortunately by the total length of the cuts). And they do so in a canonical way: isomorphic meshes will get isomorphic partitions. Therefore, an embedded graph representing the partition forms a compressed representation of the mesh that can be a lot smaller than the original input but that can be just as useful for finding matchings between meshes. Here, for instance, is the result of applying the motorcycle graph construction to three isomorphic but geometrically very different meshes, from I believe Meet the Robinsons:

Three geometrically different model heads with isomorphic meshes

In a change this year, Geometry Processing has moved to the Eurographics publishing model in which the conference proceedings is published as a special issue of a journal (Computer Graphics Forum) and the papers in it are considered to be final journal papers; there is no separate journal version. I'd be happy to email a copy of the paper to anyone who asks, but the publishers have requested that authors not make web copies available for a year after the conference. Usually I'd ignore such requests, but this time I'm inclined to agree, because I want to reward the publisher for another unusual feature of their publication: they let the authors retain copyright, and instead request an exclusive license to publish the paper, rather than demanding that the authors sign over copyright to the publisher. That's the way it is for fiction and poetry writing, and the way it should be as well for scientific writing.