Similar triangle inversion

I discovered part of the following curiosity of inversive geometry a week ago, when I was setting homework problems for my computational geometry class, and the rest of it today when the students discussed their solutions.

Claim: let \(abc\) be a right angle, and invert \(b\) and \(c\) through a circle centered on \(a\) to get points \(b'\) and \(c'\). Then triangle \(abc\) is similar to triangle \(ac'b'\). Note the permuted vertices: the right angle in the new triangle is at \(c'\)!

Proof sketch: line \(ab\) inverts to itself and contains \(b'\); line \(ac\) inverts to itself and contains \(c'\). Therefore, angle \(bac\) equals angle \(c'ab'\). Line \(bc\), which is at right angles to \(ab\), inverts to a circle \(ab'c'\), also at right angles to \(ab\). Thus \(ab'\) is the diameter of the circle and any point \(c'\) on the circle forms a right angle to this diameter. With two angles equal, the triangles are similar.

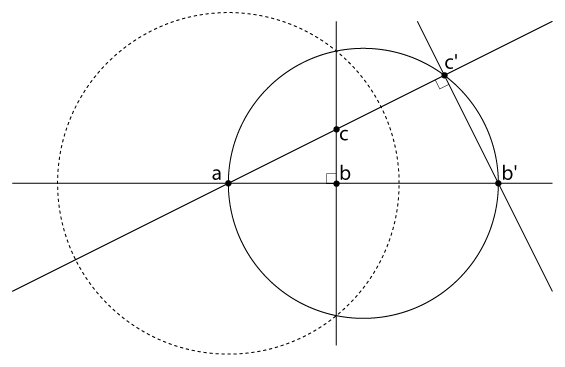
...which I thought was pretty impressive until I realized it had nothing to do with diameters and right angles. More generally, \(abc\) will always be similar to \(ac'b'\), no matter whether any angle is right, because the two triangles have one equal angle and one equal ratio of side lengths: \[|ab|/|ac| = \frac{R^2/|ac|}{R^2/|ab|} = \frac{|ac'|}{|ab'|}.\]

Oh well, despite being such a trivial piece of geometry I had fun making diagrams for it.

Comments: