The motivation for this is some work of Arvo and Novins, who showed that there exists a smooth area-preserving map between any two convex quadrilaterals (or equivalently, from any convex quadrilateral to a square), and applied the existence of such maps to stratified sampling in computer graphics. Their maps are nonlinear on the boundary of the square, so I started wondering about the existence of maps that preserve both area and perimeter. Since this doesn't seem to be making progress towards becoming a paper, I thought I'd put up my ideas on the subject here, as a way of getting them off my desktop...

Here's a simple method to find such a map. Given any quadrilateral \( ABCD \), and a point \( X \) within the quadrilateral and visible to all four edge midpoints, we can subdivide \( ABCD \) into four smaller quadrilaterals: one quadrilateral \( Q_A(X) \) with vertices \( A \), \( (A+B)/2 \), \( X \), and \( (A+D)/2 \) (that is, \( A \), \( X \), and the two edge midpoints adjacent to \( A \)), and three other quadrilaterals \( Q_B(X) \), \( Q_C(X) \), and \( Q_D(X) \) defined similarly.

Lemma: In any convex quadrilateral \( ABCD \), there exists a unique center \( X \) such that the four quadrilaterals \( Q_A(X) \), \( Q_B(X) \), \( Q_C(X) \), and \( Q_D(X) \) all are convex with equal area.

Proof: Let \( L_A \) be the locus of points \( X \) such that \( Q_A(X) \) has area \( 1/4 \) that of \( ABCD \) . Define \( L_B \), \( L_C \), and \( L_D \) similarly. \( Q_A\bigl((A+C)/2\bigr) \) is similar to \( ABCD \) but half the size; therefore \( L_A \) contains the point \( (A+C)/2 \), and it is easily seen to be a line parallel to line \( BD \). \( L_C \) contains the same point and is parallel to the same line, so \( L_A \) and \( L_C \) coincide, and similarly \( L_B \) and \( L_D \) coincide. The desired point \( X \) is at the intersection of these two lines. It must be within the convex hull of the four edge midpoints, for otherwise one of the four quadrilaterals of the lemma would be nonconvex with area smaller than the convex hull of a vertex of \( ABCD \) and two adjacent midpoints; but this convex hull is a triangle with area \( 1/4 \) of the area of a triangle formed by three vertices of \( ABCD \), which is less than \( \mathrm{area}(ABCD)/4 \). Therefore, each of the four smaller quadrilaterals is convex. QED.

It's necessary to assume convexity, as for some nonconvex quadrilaterals \( ABCD \) the entire region visible to \( A \) may have area less than a quarter that of the overall quadrilaterals, and for such quadrilaterals no such \( X \) can exist. But for convex quadrilaterals, this gives us a simple way to find an area and perimeter preserving map: find \( X \), and recursively map each of the four quadrilaterals \( Q_A(X) \), \( Q_B(X) \), \( Q_C(X) \), and \( Q_D(X) \) to the four quadrants of a square. Unfortunately the results aren't necessary very pretty:

Area- and perimeter-preserving map constructed by recursive subdivision

Here's a prettier picture of a different area and perimeter preserving map to a square for the same quadrilateral:

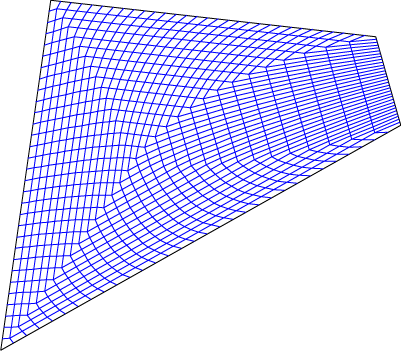
Map constructed by continuous inward motion

It's generated by a less combinatorial process, in which we shrink the input quadrilateral continuously by moving inwards the lines defining its sides, so that the shrunken quadrilateral has sides parallel to the original one. In this process, we make the speed of motion of each side line (measured perpendicularly to the line) inversely proportional to the fraction of perimeter it occupies on the shrunken quadrilateral. We parametrize each point in the quadrilateral by the time at which this shrinking process crosses the point and the position of the point along its edge of the shrunken quadrilateral containing it. Mapping points with the same parameters from different quadrilaterals produces an area and perimeter preserving map, smooth everywhere except along the four curves swept out by the quadrilateral's vertices during the shrinking process. It seems to be the only area-preserving map in which concentric squares map to quadrilaterals with sides parallel to the input quadrilateral; if so, this would imply that it's affine invariant. Like our first map, if a quadrilateral is split by a diagonal into two equal area triangles, the map is affine on each triangle.

Neither of these maps is perfectly smooth. But it's not possible for a smooth area-preserving map to a square to be linear on the boundaries of the quadrilateral, unless the quadrilateral is a parallelogram. The reason: from smoothness and linearity we can compute the area expansion at the corners to be the ratio between the area of the quadrilateral and of a parallelogram formed by the two sides of the quadrilateral. This quantity is not one at all four corners unless the quadrilateral is itself a parallelogram.




Comments:

None:
2006-03-19T20:17:36Z

Interesting.
At some point I wondered of some sort of continuous earth mover's distance between, say, two rectangles of equal area. I thought that the mapping between the two shapes should be area-preserving. Any ideas on how the cheapest mapping (in EMD sense) between two quadrilaterals looks like?

sergi(o)

11011110:
2006-03-19T21:09:55Z

By "continuous earth mover's distance" you mean \( \int |f(x)-x| dx \) for a continuous measure-preserving map \( f \) from one distribution to the other, right? So by definition it would be area-preserving, but the requirement of continuity is an addition to the usual definition of EMD.

This isn't invariant under congruences, is it? And I'm not even sure that the infimum of EMDs of continuous maps is achieved by a map that's itself continuous. E.g. consider two squares, with the same center, one turned at 45 degrees from the other. The obvious map rotates each point 45 degrees around the center, but there's a better discontinuous map that maps each point to itself in the central octagon where both squares overlap, and only does the 45 degree rotation for the points in the outer corners. It seems the EMD of this discontinuous map can be achieved as the infimum of a sequence of continuous maps with large distortion near the boundary of the central octagon.

Now I'm curious about something completely off-topic: is removing the O from your name something done in Spain generally, Catalonia, or Slovenia?

None:
2006-03-20T06:40:15Z

I would remove the condition on continuity. In EMD, weight from a point can be split to be sent to two different weights. It seems to me that this is like breaking continuity in the discrete case, so I would not ask for continuity.

Probably a best name would have been "area-preserving EMD".

Regarding my name. The Spanish version of my name is Sergio, and the Catalan one is Sergi. I have friends calling me both ways, and I felt comfortable with both namings. So, I thought that I can leave open the choice of adding the O or not, and everyone can make his or her choice. In practice, it seems that sergio is more popular, probably because it is also the spelling of the Italian version.

sergi(o)

11011110:
2006-03-20T06:54:19Z
I would remove the condition on continuity. In EMD, weight from a point can be split to be sent to two different weights.

But is splitting ever beneficial when the points are all weighted equally? It seems that the discrete unweighted case (with equal numbers of points in both distributions) is just an assignment problem, and I'd expect the case for uniform distributions over equal area polygons to be similar.