Counterexample to Ádám

A circulant is a graph, defined on the integers mod \( n \), such that for any \( x \), \( y \), and \( z \) (mod \( n \)), \( x \) and \( y \) are connected by an edge iff \( x+z \) and \( y+z \) are connected. In other words, if one draws the graph by placing the vertices in order around a circle, rotating the drawing doesn't change it. If \( G \) is a circulant, then permuting the vertices by an automorphism of the cyclic group produces another circulant; that is, we choose a multiplier \( m \) relatively prime to \( n \), and replace every vertex \( x \) by \( x*m\pmod{n} \). The Ádám Conjecture is that any two isomorphic circulants are related by a group automorphism in this way, but it turns out not to be true. I ran into a counterexample recently while playing with some code for generating circulants, but since it's not publishable (the same example was known already to Elspas and Turner in 1970 [JCT 9:229-240]), I thought I'd just share it here instead.

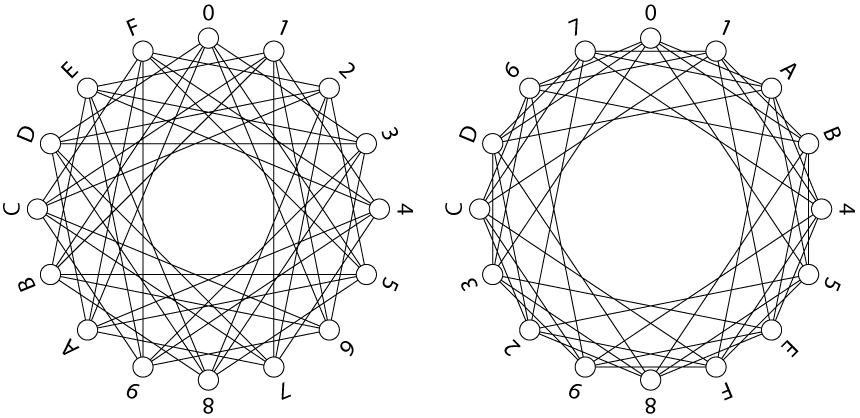
This example has 16 vertices and 48 edges. The two drawings shown are of isomorphic graphs (as can be verified tediously by comparing labels) but the isomorphism isn't realizable by any multiplication.

As it turns out, there are four different 16-vertex circulants that violate the Ádám Conjecture. The one shown here has 6 edges per vertex, and the other three have 7, 8, and 9 edges per vertex; these four graphs can be grouped into two complementary pairs.

Nevertheless, counterexamples seem rare, at least for small \( n \): they don't exist for \( n\lt 16 \), and of the 84 different 16-vertex circulants only four violate the conjecture. So, if one wants to determine whether two circulants are isomorphic, testing for multiplicative isomorphisms seems like a useful first cut to try before applying more expensive algorithms.

Incidentally, the figure formed by drawing the complete 16-vertex graph as a circulant, and extending the lines of the edges past the vertices in both directions, was familiar to ancient sailors as the pattern of rhumb lines on their portolan charts...

---

Comments: