I think most planar graphs, in some sense, should have complements with no confluent drawing, but it's been difficult to prove. Finally, I think I've found an example: the gyroelongated square dipyramid, shown below in two drawings. The left is a rough sketch of its form as a polyhedron with equilateral-triangle faces, while the right is a planar drawing.

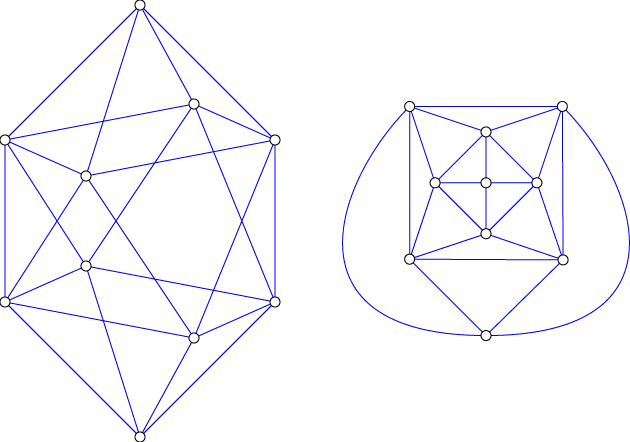
The graph of the gyroelongated square dipyramid

The proof that its complement is nonconfluent resembles that for the hypercube in our original paper on confluence. The eight degree-five vertices of the graph form a square antiprism, whose complement is a Möbius ladder with four rungs. This ladder has 4-cycles but no \( K_{2,3} \) subgraph, so (as we argued for the cube in our paper) the only possible drawings are formed by replacing some of its 4-cycles by confluent tracks. We must make an odd number of replacements in order to have a planar drawing, so essentially there are only two drawings: one with a single confluent track and one with three confluent tracks.

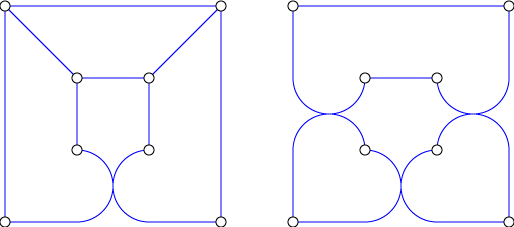
The remaining two vertices of the complement must connect to each other and to a certain subset of four vertices of the ladder, and in neither case is it possible to add tracks to the drawing that make those connections.

The regular icosahedron (aka gyroelongated pentagonal dipyramid) should make an even more symmetric example of a planar graph with nonconfluent complement, but I don't know how to prove nonconfluence in this case.